理解单纯形法，一大困难就是将数学公式、计算步骤及其实际含义对应起来，从而能够加深理解和记忆。本篇为个人电子笔记，基于Obsidian导出，参考资料附在文章末尾。

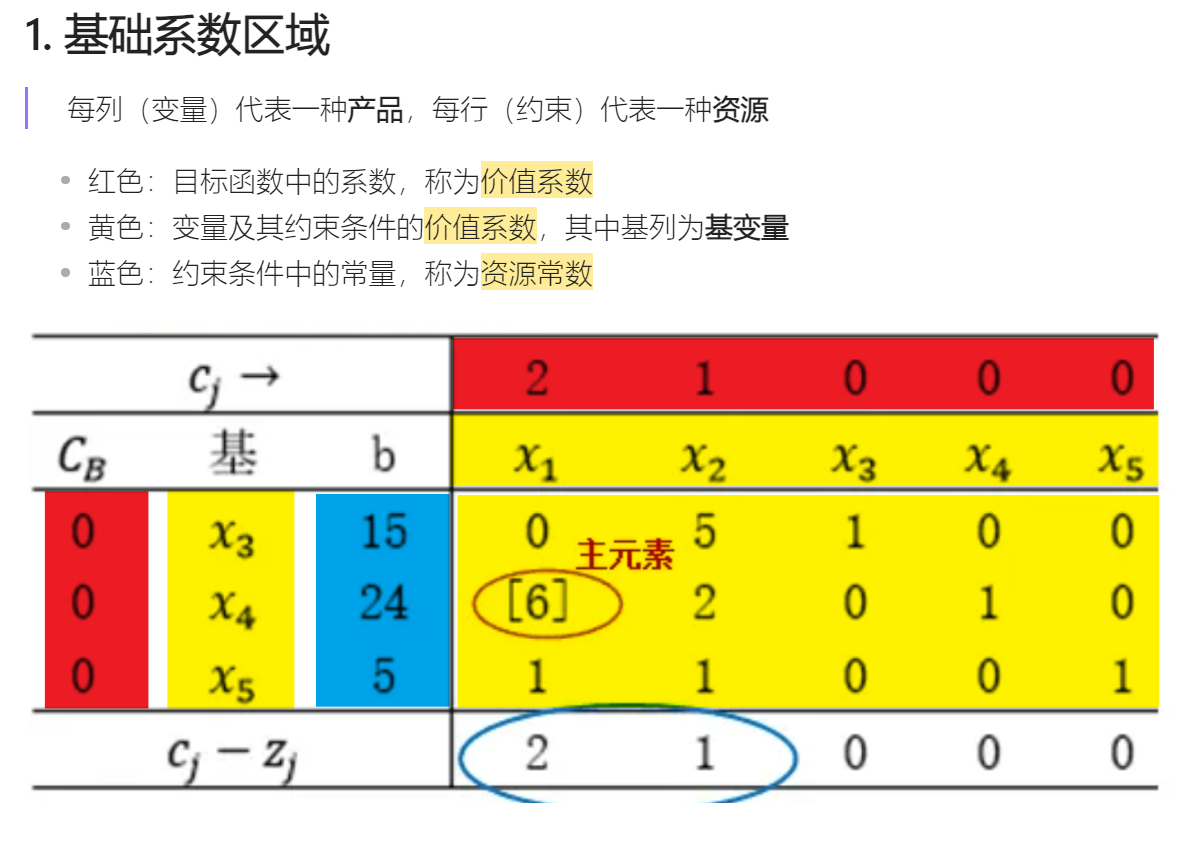
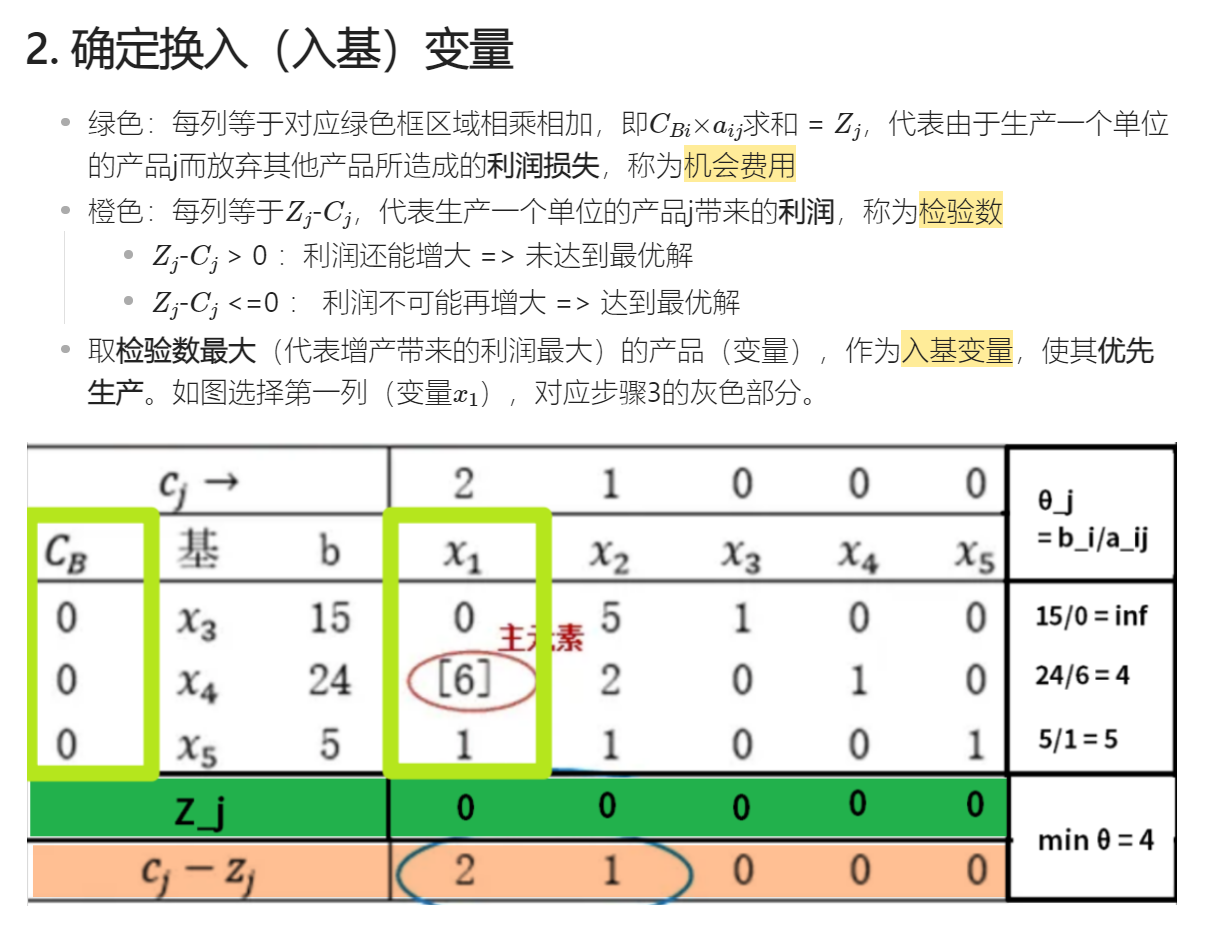
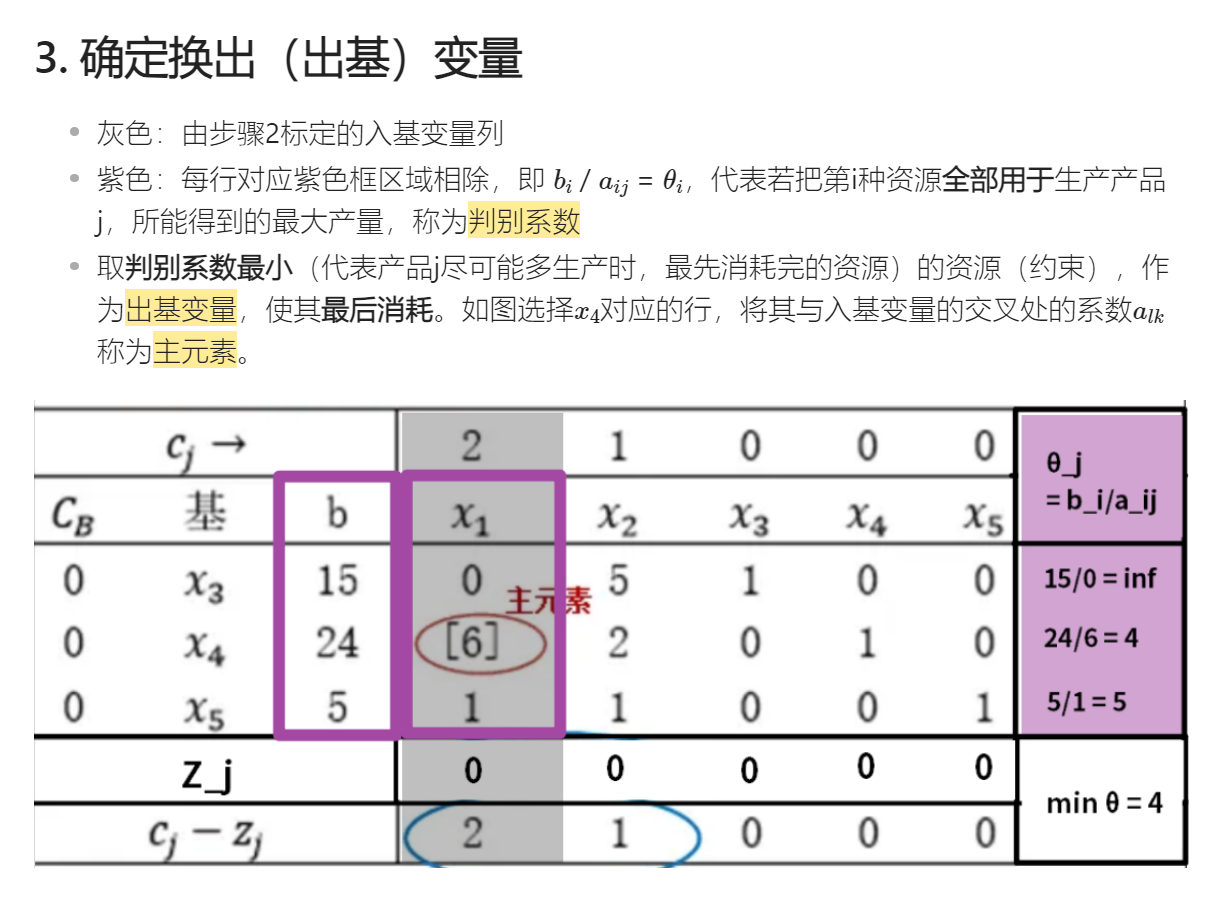
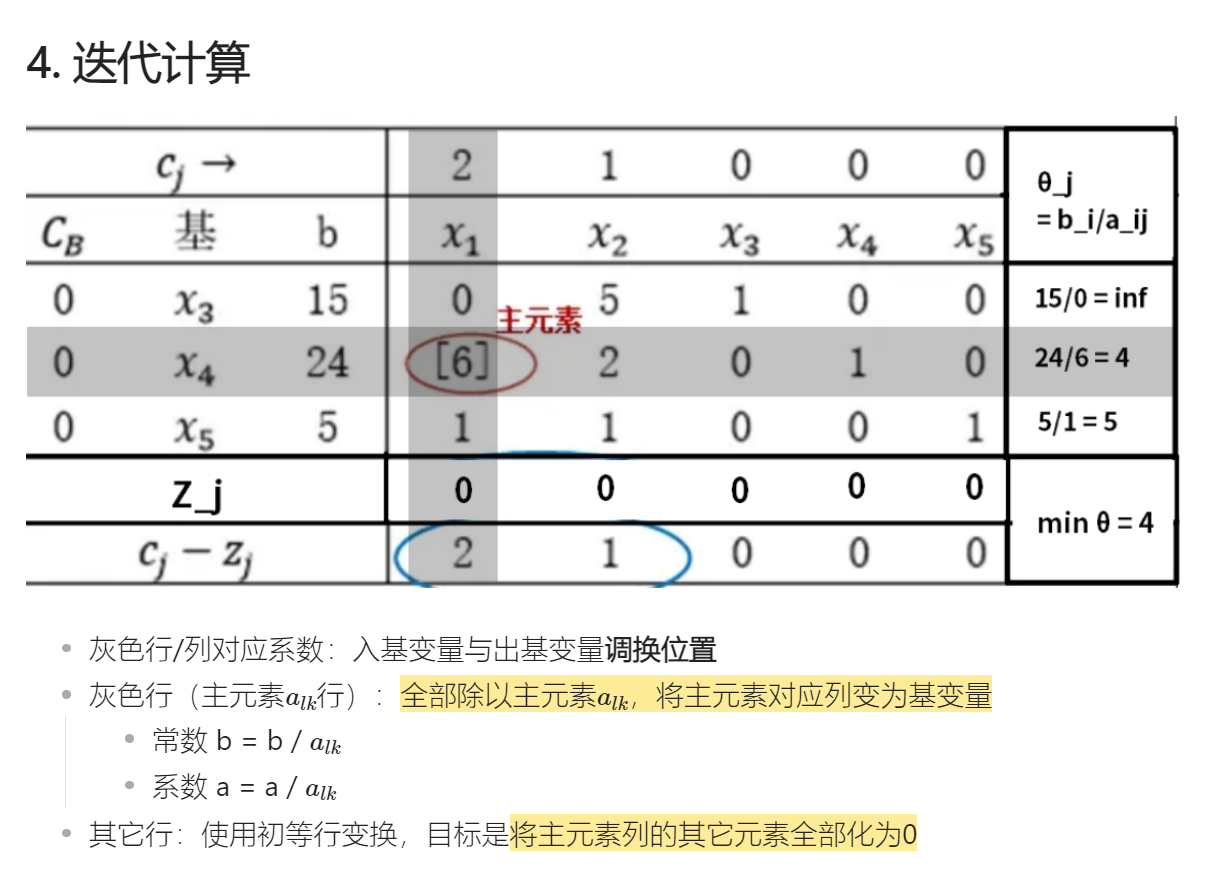
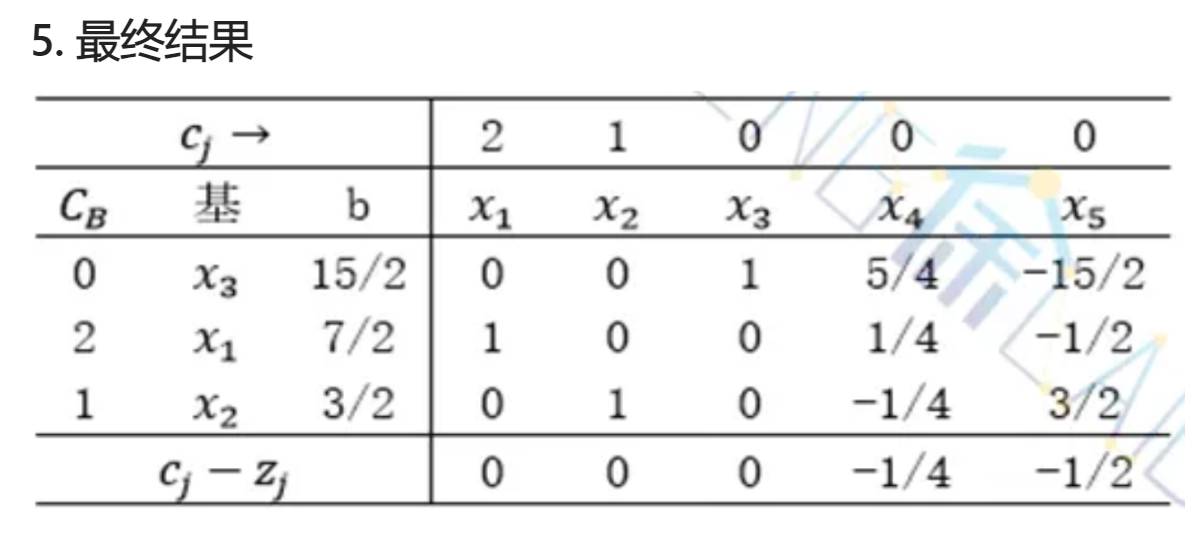
笔记正文：单纯形法基础步骤

补充：最优解判别方法

在单纯形法第2步：确定换入（入基）变量结束后，需要对检验数$Z_j$-$C_j$进行判别，从而判断是否达到最优解。流程如下：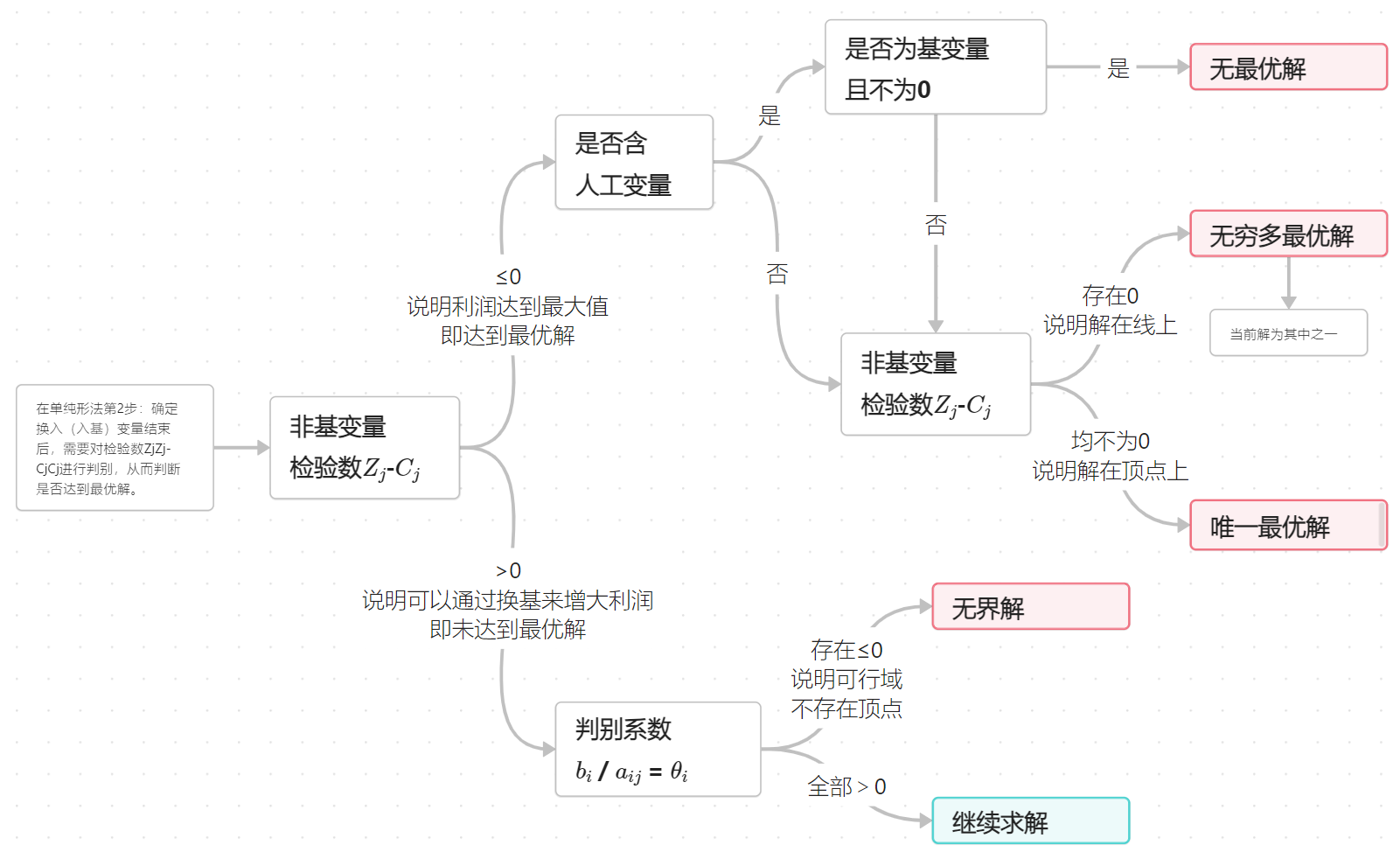

（勘误于2024.12.17）

补充：人工变量构造方法

适用条件

• 化为标准形后约束条件系数矩阵不存在单位矩阵
• 需要在约束条件中添加人工变量构造一个新的线性规划问题
• 一般情况：目标函数求最小+约束条件为$≥$

方法1：大M法

• 为构造单位矩阵，添加一个人工变量$x_5$
• 原等式本身为0 => 若存在最优解，则其不含人工变量 => 需要限制人工变量的取值
• 限制方法：在目标函数中，令人工变量系数为M（很大的正数），使得优化的目标中人工变量的惩罚系数无限大，从而保证其在优化结果中趋近于0
• 计算方式：M当做数学符号，参与单纯形法表格运算

方法2：两阶段法

添加人工变量后：

• 第一阶段：计算目标函数只含人工变量的线性规划问题 => 判断人工变量是否能从基变量迭代出去

  • 目标函数：只保留人工变量
  • 系数矩阵（约束条件）：保留所有变量不变

若基变量不含人工变量+最优目标函数值=0 => 有解 => 进行第二阶段

• 第二阶段：去除人工变量，继续迭代

  • 目标函数：只保留非人工变量，回归标准形式
  • 系数矩阵（约束条件）：只保留非人工变量

References：

• 《管理运筹学》教材 清华大学出版社2018版 何大义等著
• “运筹说”公众号文章 https://mp.weixin.qq.com/s/l2IlDb94-MKkJix1xG8--Q