引言

不可否认的是，“信息管理与信息系统”是一个延伸面极其广的专业。就其名称本身涉及到的两个方面而言，其中的“信息系统”相关的研究中，大致能分出两方面思路（研究范式）：

可以发现，前者是从以往理论出发，能够揭示内在关系；而后者从数据出发，能够发现新的规律。数据挖掘正是支持数据驱动的研究范式的重要方法。

数据挖掘一般包含以下步骤：

一、数据预处理

原因：数据存在缺失值、噪声、不一致性

一般步骤：

  1. 数据选择与集成
  2. 数据清理：处理缺失值、噪声，去除噪声、无关数据，进行数据类型的转换
  3. 数据归约：压缩、降维（包含数据离散化）
  4. 数据变换：规范化、分布聚集

描述性数据汇总

一般通过中心趋势、离散程度等来度量数据。

度量中心趋势的指标

  1. 三类均值：算数平均值、加权算术平均值、截断均值（去掉最小最大数）
  2. 中位数
  3. 众数（Mode，也叫模）

度量离散程度的指标

  1. 极差（Range，最大最小值之差）
  2. 百分位数(percentile)
  3. 方差和标准差

数据清理

  1. 空缺值：经推断而补上
  2. 噪声数据：指的是一个测量变量中的随机错误或偏差，处理方法包括分箱、回归、聚类、人工检查
  3. 数据类型的转换：通常是指连续属性离散化

数据规范化

指的是将数据按比例缩放，使之落入一个小的特定区间。主要方法有：

  1. 最小－最大规范化
  2. Z-score规范化
  3. 小数定标规范化

数据归约

数据归约：在保持原数据完整性的基础上，对这些数据进行归约化处理，以缩减数据规模、提高数据分析或数据挖掘的效果。可以用来得到数据集的归约表示，它小得多，但可以产生相同的（或几乎相同的）分析结果。

一种分类方式：

另一种分类方式：

离散化、概念分层

二、数据仓库

数据仓库是为支持管理决策建立的，面向主题的、集成的、随时间变化的、不可修改的数据集合

数据处理的类型

几个概念

三、决策树

决策树的基本结构

决策树模型构建——ID3算法

ID3算法是一种运用信息熵理论的方法。

基础：信息熵理论

熵度量了随机变量不确定性，由此在信息论中，引申出信息熵的定义：

信息熵代表每条消息/事件中，平均包含的信息量大小。它是：

  1. 数学上：信息量的期望
  2. Snipaste_2025-05-21_19-14-06.jpg

其中，2.所给出的公式中，若概率由估计方法（如极大似然估计）得出，则称计算出的熵为经验熵/条件经验熵。

引申：信息增益及其计算

描述多个变量之间的关系时，引申出信息增益的概念，即：代表得知特征X的信息时，对另一个特征Y的信息不确定性减少的程度。

在此基础上，令特征Y代表整体，即数据集D，那么其所包含的任何一个特征，都能计算出其对于整体的信息增益：

Snipaste_2025-05-21_19-19-41.jpg

对于决策树来说，其关键在于决定用哪个特征来得到分支，即划分特征空间，又称为特征选择。信息增益可以作为特征选择的重要依据，因为某一层决策的信息增益越高，整个分类的不确定性就越低。

ID3算法的计算步骤

给定训练数据集D

  1. 计算整个数据集的经验熵 H(D)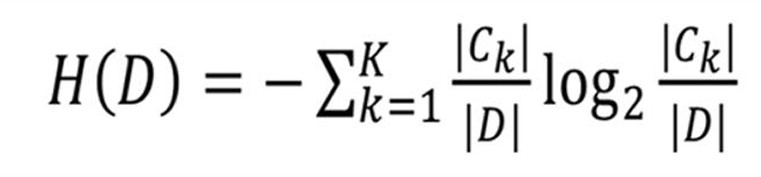：Snipaste_2025-05-21_19-31-08.jpg其中，k代表每个类别，$|C_k|$ 则是当前类别下的条目数。特别注意，信息熵公式的负号不能遗漏。
  2. 对于特征A的每个类别i，分别计算信息熵 H($D_i$)：公式同1.
  3. 对于特征A，根据3.计算其对于数据集D的经验条件熵 H(D|A)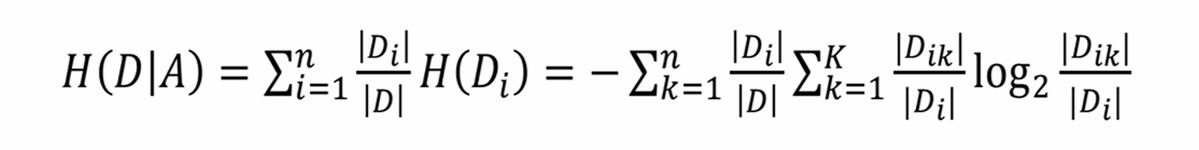：Snipaste_2025-05-21_19-35-55.jpg也即对类别i信息熵的加权平均
  4. 根据3.的结果，计算信息增益 $g(D,A) = H(D) - H(D|A)$
  5. 对每个特征A，重复步骤2.3.4.，取所有特征中信息增益最大的为根节点，得到分支
  6. 利用剩余特征，对相应分支的数据集重复上述步骤，直到所有特征选择完毕，得到完整的决策树

选择当前样本集中具有最大信息增益值的属性作为测试属性，即该测试属性为决策树的非叶节点

下面提供一道例题：
使用ID3决策树算法对下面两个未知类型的样本进行分类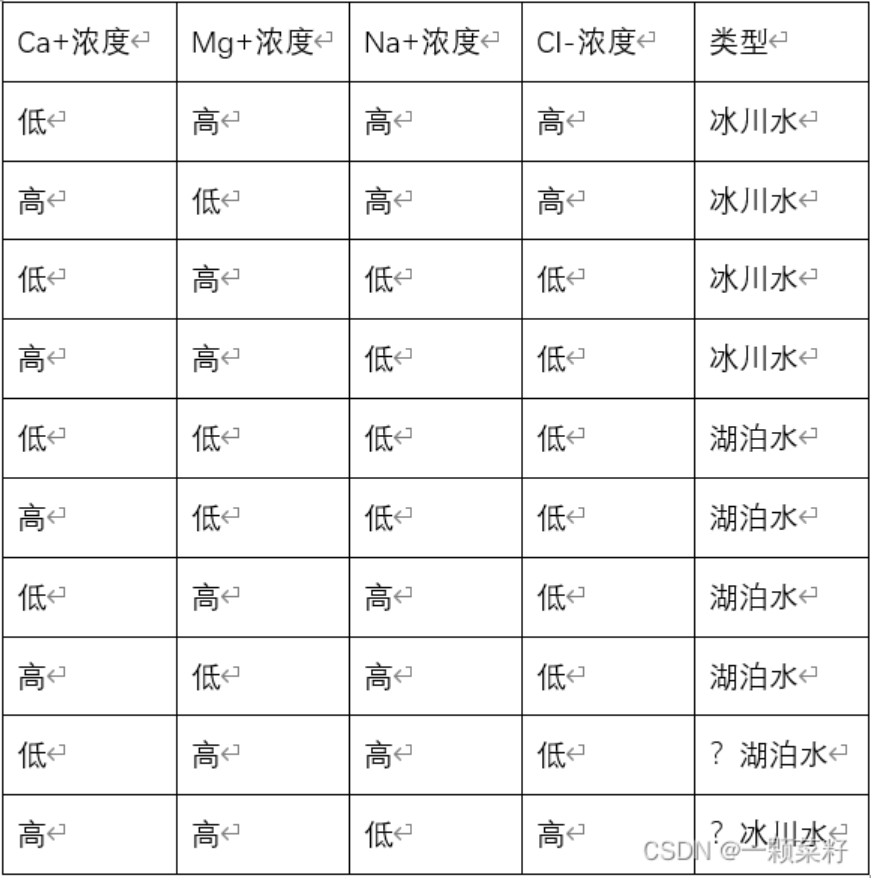
Snipaste_2025-05-26_22-54-53.jpg

解答步骤如下：
Snipaste_2025-05-26_22-56-40.jpg

过拟合与过抽样

训练样本中的错误数据也会被决策树学习，成为决策树的部分，这样一来导致测试数据的表现不佳，称为过拟合(Overfitting)问题。表现为在训练集上拟合效果很好,而在测试集上的预测效果很差。

同时，训练样本中若类别过于不平衡，则会同样导致模型存在过拟合，由此引入过抽样方法：指的是在样本很少的时候，添加或者复制样本，通过增加样本中小类样本的数据量来实现样本均衡，从而改善模型训练效果。

四、聚类

聚类与分类的区别

分类属于有监督学习，需要首先通过训练集训练分类模型，其中每个训练样本有一个类别标记，是利用一个分类函数（分类模型、分类器），把数据库中的数据映射到给定类别中的一个

而聚类属于无监督学习，没有训练集、类别标记，是根据最大化簇内相似性、最小化簇间相似性原则，按数据对象之间的相似性将对象分组，得到的每个组称为类或簇（cluster）。

分类

  1. 划分法：大多是基于距离的
  2. 层次法
  3. 密度聚类方法
  4. 网格聚类

K-means算法

对于包含n个对象的数据集D，目标是将其分为k个簇。步骤如下：

  1. 从D中任意选择k个对象作为初始簇中心
  2. 计算每个簇中对象的均值
  3. 将每个对象分配到最相似的簇
  4. 更新簇均值，即重新计算每个簇中对象的均值；
  5. 重复步骤2.3.4.直到不再发生变化
  6. 掌握聚类分析的统计量
  7. 熟悉聚类算法的各个类别。
  8. 熟练掌握K-means的计算算法。
  9. 掌握基于划分与基于层次的聚类方法基本流程与各自的优缺点。

五、关联规则

关联规则的原理

关联规则的定义

关联规则描述数据库中各数据项之间存在的潜在关系，形式为X=>Y（X称为规则头antecedent，Y称为规则尾consequent），其中：

实际应用中：

项的出现频率——支持度

对于数据项X，其在事务集合D中的出现次数称为支持数，那么可以定义：其在事务集合D中的出现概率Pr(X)为支持度，即 support(X)= X的支持数 / 事务集合D的总事务数 。

为了表示数据项的最低重要性，定义支持阈值s，常用最小支持度minsup代替。由此，如果项集X满足：

则X称为大项集(large itemset) 或者频繁项集(frequent itemset）。进一步地，按频繁项集中数据项X包含的元素个数n，将其称为n阶频繁项集。

同时出现的可能性——置信度

事务集合D中，包含事务X的同时也包含事务Y的可能性，称之为置信度（confidence），记作conf(X=>Y)。它的本质是条件概率，公式如：

conf(X=>Y) = Pr(Y|X) = Pr(X∪Y)/Pr(X) = (X∪Y)的支持度/X的支持度

类似地，引入置信阈值minconf表示关联规则的置信度。

对于某个关联规则，若其支持度、置信度均大于等于其阈值，则该关联规则为强关联规则。这是从数据库（即事务集合D）中识别关联规则的基础。

关联规则挖掘方法

一般步骤

  1. 频繁项集的搜索：按某种方式扫描数据库
  2. 生成关联规则：对于每个频繁项集L，选取其所有非空子集X，逐个生成并检查规则X=>L-X是否符合要求

大部分关联规则挖掘方法的区别都在1.，Apriori算法利用上次循环产生的频繁项集构造新的候选项集，较为常用。

Apriori算法

其原理是：频繁项集的子集，也是频繁项集。利用此原理，首先进行频繁项集的搜索，步骤如下：

  1. 逐行（事务）扫描，针对每个元素（n=1）给出支持数：即数出每个元素的总出现个数
  2. 识别出n阶频繁项集：将1.中得到的支持数与最小支持度阈值对比，保留大于等于的
  3. 连接：由之前的频繁项集，循环各个项构造交互项，得到新的集合
  4. 剪枝：针对步骤3.的每个交互项，若该项的任意一个子集不属于步骤2.的n阶频繁项集，则将该交互项剪去
  5. 识别出n+1阶频繁项集：针对4.得到的集合，重复步骤2.，直到4.剪枝后为空

由此得到多个不同阶数的频繁项集后，进行关联规则的生成，步骤如下：

  1. 对于每个频繁项集：写出其全部真子集，如对于{ABC}，其真子集为{A}{B}{C}{AB}{AC}{BC}
  2. 对于1.产生的真子集：构造交互项（连接），保留字母不同的（剪枝），得到{A}{BC}、{B}{AC}、{C}{AB}
  3. 对于2.产生的交互项：构造两个方向的规则，即：
    {A}{BC}：A=>B∧C，B∧C=>A
    {B}{AC}：B=>A∧C，A∧C=>B
    {C}{AB}：C=>A∧B，A∧B=>C
  4. 对于每个规则，计算其置信度conf(X=>Y)=Pr(X∪Y)/Pr(X)，即当前频繁项集的频率/n-1频繁项集的对应元素频率
  5. 将置信度逐个与置信阈值比较，大于等于其的记为强关联规则

六、序列模式
1、掌握序列模式的定义与具体应用。
2、掌握序列模式与关联规则的区别。
3、熟悉哈希树的概念。